Zufallszahlen
Referat in der Lehrveranstaltung
Algorithmen und Komplexität
von Thiemo Kreuz und
Sebastian Lüth,
II99, vorgetragen am 06.06.2001
"Jedermann, der Zufallszahlen mit einer arithmentischen Methode erzeugen will, ist nicht ganz bei Trost." (John von Neumann, 1951)
1. Begriffe
- Zufall ist ein Ereignis, dass mit einer gewissen Wahrscheinlichkeit eintreten kann, jedoch nicht eintreten muss.
- Zufallszahlen sind Zahlen, die aus Zufallsexperimenten gewonnen werden.
- Pseudozufallszahlen sind Zahlen, die mit mathematischen Algorithmen erzeugt werden.
2. Anwendungsgebiete
- Kryptographie, zur Generierung von Schlüsseln
- Simulationen, Tests
- Entscheidungsfindung (z.B. wenn zwei Wege genau gleich wahrscheinlich sind)
- Stichproben
- Spiele, Effekte (Beispielprogramm blitz.exe zur Visualisierung)
3. Generierung echter Zufallszahlen
- Glücksspiele (Würfeln, Roulette, Münze werfen, ...)
- Emmisions-Generatoren (Kernzerfall radioaktiver Elemente, bekannt ist nur die Wahrscheinlichkeit des Zerfalles - die Halbwertszeit)
- Signalrauschen, z.B. thermisches Rauschen von Widerständen (neuerdings in Serie auf Intel's i810 Chipsatz)

- Tastenanschläge, Mausbewegung, Zeit zwischen Festplattenzugriffen oder Interruptaufrufen, ...
4. Eigenschaften von Zufallszahlen
- Unvorhersehbarkeit. Nur eine Voraussage mit einer bestimmten Wahrscheinlichkeit ist möglich.
- Gleichverteilung. Jeder Wert in einem bestimmten Intervall besitzt ungefähr die gleiche relative Häufigkeit.
- Unabhängigkeit. Keine Zahl hängt von einer anderen ab.
5. Generierung von Pseudozufallszahlen
- Computer sind deterministische Maschinen
- Pseudozufallszahlen werden durch streng deterministische Algorithmen erzeugt
- sind also eigentlich gar nicht zufällig
- haben allerdings die wichtigsten Eigenschaften von echten Zufallszahlen (Unvorhersehbarkeit, Gleichverteilung, jedoch nicht Unabhängigkeit, da in der Regel die folgende Zahl aus der aktuellen berechnet wird)
- Generierung ist mit wesentlich geringerem Aufwand verbunden (nur Soft- und keine Hardware)
- generiert werden immer Zahlen aus einem begrenzten Intervall (z.B. Doppelworte zwischen 0 bis 232-1 oder Fließkommazahlen zwischen 0 bis 1)
- in der Regel werden Folgen von Zufallszahlen generiert (rekursive Algorithmen), einzelne Zufallszahlen sind ein Sonderfall davon
- da jede Zufallszahl zi zu einer bestimmten Zahl zi+1 führt, der Wertebereich jedoch begrenzt ist, ist jeder Zufallszahlengenerator periodisch
- eine weitere Forderung ist somit eine große Periodenlänge
6. Algorithmen zur Berechnung von Pseudozufallszahlen
6.1. Middle-Square-Generator
- 1949, John von Neumann
- 2k-stelliger Startwert
- quadrieren
- evtl. vorn mit Nullen auffüllen, so dass ein 4k-stelliger Wert entsteht
- die mittleren 2k Stellen bilden die nächste Zufallszahl
- Beispiel: 62*62=3844 -> 84*84=7056 -> 5*5=0025 -> 2*2=0004 -> 0*0=0000 -> ...
- zi+1 = floor(zi2/gk) - floor(zi2/g3k) * g2k
- g ist die Zahlenbasis, beim Computer sinnvollerweise 2, somit ergibt sich die vereinfachte Form:
zi+1 = (zi2 shr k) - ([zi2 shr 3k] shl 2k) - Vorteile: einfache Implementierung
- Nachteile: sehr hoher Rechenaufwand, sehr kurze Periodenlänge, stürzt oft auf Null ab
- besitzt somit nur noch historische Bedeutung
6.2. Eumel-Generator
- nur ein Beispiel für viele der auf irrationalen Zahlen basierenden Generatoren
- entwickelt 1984 für das gleichnamige Betriebssystem
- zi+1 = (Pi + zi)8 - floor[(Pi + zi)8]
- wesentlich bessere Periodenlänge als Middle-Square, aber noch nicht wirklich brauchbar
6.3. Schieberegister-Generatoren
- auch "Additive Kongruenz" genannt
- Schieberegister mit n Positionen, das mit beliebigen Binärziffern initialisiert wird (jedoch nicht alles Null)
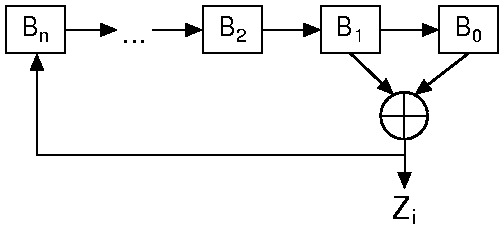
- pro Durchgang Verschiebung um eine Stelle nach rechts
- das frei werdende Bit wird durch die Verknüpfung zweier anderer Positionen berechnet (z.B. XOR mit den Bits 0 und 1)
- Periodenlänge bis zu 2n-1
- gute Zufallsgeneratoren für große n
- Qualität ist stark von der Wahl der beiden Abgriffspositionen abhängig
- möglich ist auch die Verwendung von n ganzen Zahlen, die dann auch mit ADD anstatt XOR verknüpft werden können (JavaScript-Beispiel)
- Anwendung heute nur noch in Hardwareimplementierungen aufgrund des hohen Speicherbedarfes
6.4. Lineare Kongruenzmethode
- die heute am meisten verwendete Methode
- entwickelt 1951 von D. H. Lehmer
- zi+1 = (a * zi + b) mod m
- b kann Null sein, dann nennt man das Ganze "multiplikativ", ansonsten "gemischt"
- Qualität hängt sehr stark von der Wahl der Parameter a, b, m und z0 ab
- Periode ist maximal m-1, aus diesem Grund sollte man m möglichst groß wählen
- es wurden verschiedene Richtlinien für optimale Startparameter entwickelt
- m sollte eine Zweier- oder Zehnerpotenz sein
- b sollte kleiner als m sein (im Allgemeinen eine Ziffer kleiner)
- b sollte auf ...x21 enden, wobei x eine gerade Zahl sein sollte (Empfehlung von D. E. Knuth)
- wenn m eine Primzahl und b = 0 ist, wird für bestimmte a die maximale Periodenlänge erreicht
- die Periodenlänge ist maximal für a = 2k + 1 (2 <= k < t), b = 1 und m = 2t (t >= 3)
- PHP-Beispiel zum Experimentieren
- Codebeispiele aus diversen Programmiersprachen
7. Komplexität
- Zufallszahlengeneratoren basieren auf sehr simplen Operationen
- zur Generierung von Reihen werden Schleifen eingesetzt
for (int x=1; x<n; x++) { Zufallszahlenalgorithmus; } - somit gilt O = (n), das heißt der Zeitbedarf steigt proportional zur Anzahl der generierten Zufallszahlen
- Speicherbedarf ist beim Middle-Square-Generator sehr gering, dafür ist der Rechenaufwand sehr hoch
- beim Eumel-Generator hoher Rechenaufwand durch die Potenzierung mit 8 und die Verwendung der (eigentlich irrationalen) Zahl Pi
- Speicherbedarf steigt beim Schieberegister-Generator proportional mit der Bit-Anzahl des Schieberegisters. Der Rechenaufwand steigt proportional zur Anzahl der Zufallszahlen, hinzu kommt ein konstanter Aufwand für die Initialisierung
- bei der Linearen Kongruenzmethode ist der Rechenaufwand höher, steigt aber ebenfalls linear
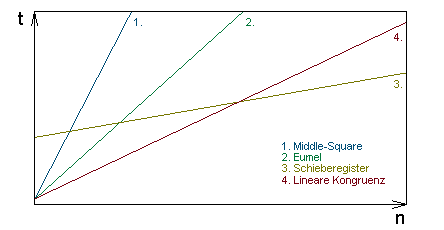
- somit empfiehlt sich für große Mengen von Zufallszahlen die Schieberegister-Methode (sofern der Speicherbedarf vernachlässigbar ist), andernfalls sollte immer die Lineare Kongruenz angewandt werden
8. Quellen
- Hillebrand: "Zufallszahlen - Methoden der Generierung, Schwächen, Verwendung", http://www.logic.at/lvas/krypto/Hillebrand/html
- Ranzinger: "Stochastische Algorithmen und deren Anwendung - Zufallszahlen", http://www.inf-gr.htw-zittau.de/~wagenkn/TI/Komplexitaet/ReferateSS00/ranzinger.pdf
- Freitag: "Spinoffs", http://hlhp1.physik.uni-ulm.de/users/freitag/spinoffs2.html
- Wetzel: "Zufallszahlen erzeugen - Methode der linearen Kongruenz", http://educeth.ethz.ch/informatik/werkstatt/multiplik/zufallszahlen
- Deley: "Computer Generated Random Numbers", http://world.std.com/~franl/crypto/random-numbers.html
Codebeispiele
' Programmbeispiel Basic ' liefert Pseudozufallszahlen 0 <= x < 100 RANDOMIZE TIMER FOR i = 1 TO 10 PRINT RND * 100 NEXT
<script>
// Programmbeispiel JavaScript
// liefert Pseudozufallszahlen 0 <= x < 100
for (i=1; i<=10; i++) {
document.write( Math.random() * 100 );
document.write( "<br>" );
}
</script>
{ Programmbeispiel Pascal
liefert Pseudozufallszahlen 0 <= x < 100 }
var i: integer;
begin
randomize;
for i := 1 to 10 do
writeln( random(100) );
end.
#!/usr/bin/perl
# Programmbeispiel Perl
# liefert Pseudozufallszahlen 0 <= x < 100
print "Content-type: text/plain\n\n";
for ($i=1; $i<=10; $i++) {
print rand(100) . "\n";
}
<?php
// Programmbeispiel PHP
// liefert Pseudozufallszahlen 0 <= x < 100
srand ( (double)microtime() * 1000000 );
for ($i=1; $i<=10; $i++) {
echo rand(0,100) . "<br>";
}
?>