Thiemos Archiv
I used to have a weblog and a personal homepage here since 1999. In 2022 I moved to thiemokreuz.de.
- Sunday, 2007-11-18 23:07
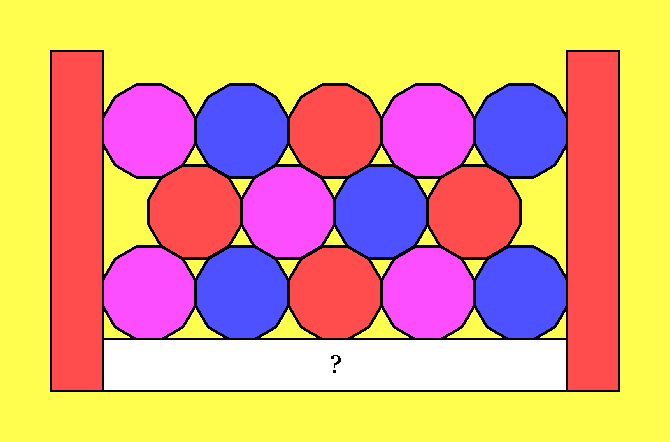
- Ich bin auf eine nette kleine Art von Rätseln gestoßen, die wirklich knifflig sein können, obwohl die Regeln sehr schlicht sind. Die Aufgabe besteht darin, eine vorgegebene Flächenaufteilung mit nur vier Farben so zu füllen, dass sich nie zwei gleichfarbige Flächen berühren. Als einzige Ausnahme sind Berührungen an einer Ecke erlaubt (im hier gezeigten Beispiel kommt das nicht vor). Mit dieser simplen, aus dem Vier-Farben-Satz (früher auch »Vier-Farben-Vermutung«) stammenden Regel lassen sich nun zwei Arten von Aufgaben konstruieren. Zuerst kann man versuchen, Lösungen für vorgegebene Vier-Farben-Rätsel zu finden.
Das hier gezeigte Bild stellt einen Behälter dar, der mit Sand (stark vergrößert) oder Bällen gefüllt ist, die sich gegenseitig berühren. Betrachtet man nur die Sandkörner und lässt den Behälter und die Luft zwischen den Sandkörnern außer Acht, stellt man fest, dass man drei Farben für die Füllung benötigt. Die Luft erhält die vierte Farbe. Für den Behälter bleibt nun scheinbar keine Farbe mehr übrig.
Um dennoch eine Lösung finden zu können (die dem – übrigens mathematisch bewiesenen – Vier-Farben-Satz zufolge immer existieren muss), ist es erlaubt und sogar erforderlich, bereits ausgefüllte Flächen umzufärben. Eine der möglichen Lösungen für das oben gezeigte Rätsel kann hier eingesehen werden.
Hat man das geschafft (am besten natürlich, ohne sich die Lösung anzusehen) kann man als nächstes versuchen, neue Vier-Farben-Rätsel zu schaffen, die den Betrachter in die Irre führen und möglichst schwer zu lösen sind. Der Leser sei jedoch gewarnt: Es ist verlockend, nach einer Flächenaufteilung zu suchen, die sich unmöglich mit nur vier Farben füllen lässt. Solche vermeintlichen Unmöglichkeiten beruhten jedoch immer auf ungültigen Annahmen. In der oben gezeigten Sandkiste war es beispielsweise unzulässig, der Luft zwischen den Bällen eine feste Farbe zuzuordnen. Damit schafft man das, was auf Landkarten »Exklaven« genannt wird, und bewegt sich damit bereits außerhalb der engen Definition des Vier-Farben-Satzes.
Kommentare zu diesem Beitrag können per E-Mail an den Autor gesandt werden.
http://wiesbaden.kijiji.de/c-Kaufen-Verkaufen-PC-Videospiele-Vier-Farben-Raetsel-W0QQAdIdZ30380079
Gruß,
daher eher in der Größenordnung von 47.784.725.839.872.000 vermutet werden. Aber wenn jemand behauptet der Mathematiker X habe etwas bewiesen, wird dies selten kritisch hinterfragt. In Wahrheit wird erst erkennbar, ob es es Lösung gibt, wenn man konkret beginnt Zahlen einzusetzen und erst am Schluss sieht man, ob es aufgeht. Die Zahl der Lösungen beim Sudoku ist unbekannt, ebenso wie der Vierfarbensatz höchst wahrscheinlich falsch ist.